Матрица поворота в двумерном пространстве. Поворот системы координат на угол, матрица вращения Поворот в двумерном пространстве
Преобразования в трех мерной системе координат
В трех мерной системе координат используются следующие базовые преобразования:
Перенос точки на заданный вектор;
Поворот на заданный угол относительно координатной оси;
Перенос системы координат на заданный вектор;
Поворот системы координат на заданный угол относительно координатной оси;
Зеркальное отображение точки относительно координатной плоскости XY ;
Зеркальное отображение точки относительно плоскости XY ;
Зеркальное отображение точки относительно координатной оси XZ ;
Смена направление координатной оси;
Изменение масштаба координат по оси X ;
Изменение масштаба координат по оси Y .
Изменение масштаба координат по оси Z .
Перенос точки на вектор U , задаваемый параметрами u x , u y , u z , предполагает следующее преобразование координат:
x a’ = x a - u x ;
y a’ = y a – u y ;
z a ’ = z a – u z .
Используя однородную систему координат, данные преобразования в матричной форме можно представить в виде:

a ,b ,c – параметры вектора переноса.
Легко показать, что матрица обратного преобразования (или матрица переноса системы координат) в этом случае будет иметь вид:

Поворот относительно координатной оси.
Поворот относительно оси Z .
Данный вид преобразования иллюстрируется ниже приведенным рисунком (Рис. 5.2‑1), где приводится поворот точки А на угол a .
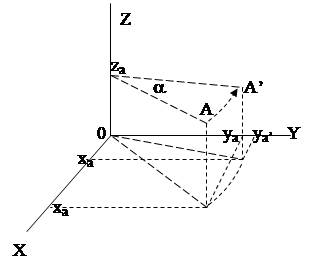 |
Рис. 5.2 ‑ 1
Из приведенного рисунка видно, что поворот относительно оси Z не меняет координаты точки по координатной оси Z . Что же касается изменений координат по оси X и Y , то они аналогичны изменениям по осям X ,Y в двумерной координатной системе, так как новая и старая точки остаются в одной плоскости, параллельной координатной плоскости X ,Y . Таким образом, использую уравнения (5.1-5) и (5.1-6), будем иметь:
x b ’ = x b cos a - y b sin a + 0;
y b’ = x b sin a + y b cos a +0;
z b ’ = 0 +0 +z .
Данные преобразования можно представить в матричной форме как:
 (5.1-7)
(5.1-7)
Поворот относительно оси X .
Координатные оси в трехмерной системе равнозначны, поэтому поворот относительно координатной оси X , аналогично повороту относительно оси Z , можно представить как:
y b’ = y b cos a - z b sin a + 0;
z b’ = y b sin a + z b cos a +0;
x b ’ = 0 +0 +x .

Для того, чтобы координаты матриц перечислялись в том же порядке, что и в выражении (5.1-7), необходимо их циклически сдвинуть в сторону элемента с большим индексом, т.е. вправо. При этом соответствующий сдвиг необходимо выполнить и в матрице начальных координат. Что же касается двумерной матрице, то ее колонки необходимо циклически сдвинуть вправо (в сторону колонки с большим индексом), а затем циклически сдвинуть строки вниз (в сторону строки с большим индексом), как это показано ниже.
 (5.1-8)
(5.1-8)
Поворот относительно оси Y .
Координатные оси в трехмерной системе равнозначны, поэтому поворот относительно координатной оси Y , аналогично повороту относительно оси Z , можно представить как:
z b ’ = z b cos a - x b sin a + 0;
x b ’ = z b sin a + x b cos a +0;
y b ’ = 0 +0 +y .
Соответственно в матричной форме будем иметь:

Для того, чтобы координаты в матрице перечислялись в том же порядке, что и в выражении (5.1-7), необходимо их циклически сдвинуть в сторону элемента с меньшим индексом, т.е. влево. При этом соответствующий сдвиг необходимо выполнить и в матрице начальных координат. Что же касается двумерной матрице, то ее колонки необходимо циклически сдвинуть влево (в сторону колонки с меньшим индексом), а затем циклически сдвинуть строки вверх (в сторону строки с меньшим индексом), как это показано ниже.
 (5.1-8),
(5.1-8),
Таким образом, матрицы базового поворота на угол a по отношения к координатной оси будут иметь вид:


 (5.1-9),
(5.1-9),
Легко показать, что матрицы соответствующих обратных преобразований (или матрицы поворота системы координат относительно координатных осей), будут иметь вид:


 (5.1-10)
(5.1-10)
Зеркальное отображение точки относительно координатной плоскости XY .
зависимости координат.
Для отображения относительно координатной плоскости XY :
x a’ = x a
Y a’ = y a ;
Z a’ = -z a .

Для отображения относительно координатной плоскости XZ ;
x a’ = x a
Y a’ = - y a ;
Z a’ = z a
В матричной форме это преобразование записывается как:

Для отображения относительно координатной плоскости ZY :
x a’ = -x a
Y a’ = y a ;
Z a’ = z a .
Матричная запись будет иметь вид:

Смена направления координатной осей
Преобразование координат при смене направленности координатных осей X ,Y ,Z отображается, соответственно, следующими матрицами.



Изменение масштаба по координатным осям .
Преобразования этого типа предполагает следующие зависимости координат:
x a’ = r x a ;
Y a’ = l y a ;
Z a ’ = f z a ,
где r , l , f – вводимые масштабные коэффициенты по соответствующим координатным осям.
В матричной форме это преобразование записывается как:

Рассмотрим сложное преобразование координат в трехмерной системе.
Предположим необходимо выполнить поворот точки относительно произвольного вектора в трех мерной системе координат, как это показано на Рис. 5.2‑2.
Сначала решим рассматриваемую задачу для частного случая. Предположим, что вектор U , относительно которого нужно повернуть точку А на угол a , проходит через начало системы координат (Рис. 5.2‑3).
Вектор, относительно которого необходимо выполнить поворот, можно задать в сферических координатах, т.е. через тройку параметров: q, j, r, где:
R - модуль вектора U ;
J - угол между вектором U и координатной осью Z ;
Q - угол между проекцией r ’ вектора U на координатную плоскость XY и координатной осью X .

Рис. 5.2 ‑ 2
При таком частном случае заданное преобразование поворота точки относительно заданного вектора можно выполнить за счет последовательности следующих базовых преобразований:
1)поворот исходной системы координат относительно координатной оси Z на угол q ;
2)поворот новой системы координат относительно оси Y на угол-j ;
3)поворот точки А относительно координатной оси Z ’’на угол a ;
4)поворот системы координат на угол j относительно оси Y ;
5) поворот системы координат относительно координатной оси Z на угол-q .
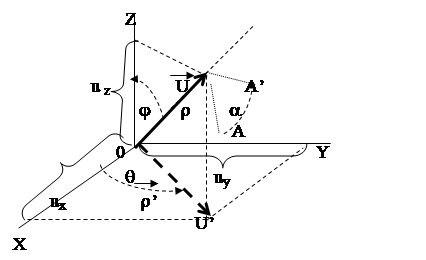 |
Рис. 5.2 ‑ 3
1-ый поворот исходной системы координат относительно ее оси Z на угол q формирует новую систему координат X ’Y ’Z ’, в которой ось X ’ совпадет с r ’, ось Y ’ будет повернута по отношению к оси Y на угол q , ось Z ’ совпадает с осью Z , что показано на Рис. 5.2‑4.
 |
Рис. 5.2 ‑ 4
Отметим, что в новой системе координат вектор U лежит в координатной плоскости X ,Z .
Поворот осуществляется при использовании матрицы обратного преобразования типа «поворот относительно координатной оси Z ».
2-ой поворот формирует систему координат X ”Y ”Z ”, в которой ось X ” повернута относительно оси X ’ на угол (-j ) (угол поворота отрицательный, так как для совмещения оси Z новой системы координат с вектором U поворот нужно выполнить в направлении по часовой стрелке), ось Y ’’ совпадает с осью Y ’, ось Z ” совпадает с вектором U .
Рассматриваемому повороту соответствует матрица базового поворота точки относительно оси Y .
3-ий поворот. В системе координат, полученной после выполнения двух предыдущих поворота, заданный вектор U совпадает с осью Z ”, что позволяет выполнить в этой системе заданный поворот за счет базового поворота относительно оси Z ”.
4-ый поворот обеспечивает возврат к системе координат X ’,Y ’,Z ’ и реализуется с помощью матрица обратного преобразования типа «поворот относительно координатной оси Y » на угол j .
5-ый поворот обеспечивает возврат к начальной системе координат X ,Y ,Z и реализуется с помощью матрица преобразования типа «поворот относительно координатной оси Z » на угол -q .
Таким образом, формирование координат точки при рассматриваемом сложном преобразовании осуществляется через произведение матриц элементарных преобразований следующего вида:
 (5.1-10)
(5.1-10)
X и , y и , z и – исходные кордиинаты точки;
X пч , y пч , z пч – новые кордиинаты после поворота для рассматриваемого частного случая;
-

-

-

-

-
При решении рассматриваемой задачи для общего положения в пространстве вектора U , используется те же действия, что и в рассмотренном частный случай, с добавлением в начале преобразований перенос исходной системы координат в точку D (см Рис. 1.2‑1) и в конце - перенос начало координат из точки D в точку начала координат исходной системы.
Таким образом, для общего положения вектора поворота, новые координаты точки А после заданного поворота определяются через произведение матриц элементарных базовых преобразований следующим образом:
(5.1-11)
x п, y п, z п - координаты положения точки после поворота;


Переход от одной формы задания вектора к другой.
Вектор, который часто используется в процессе преобразований координат, иногда удобно задавать в полярных координатах (например, при поворотах), а иногда в декартовых координатах (например, при переносах). На практике вектор задается только одним из этих способов. Для перехода от одной формы задания вектора к другой используются следующие соотношения.
Переход от декартового к полярному представлению вектора
При задании вектора U в полярных координатах в виде тройки {r,j,q}, как следует из Рис. 5.2‑3, имеет место:
u z =r cos j ;
u x =r sin j cos q ;
u y =r sin j sin q ;
Переход от полярного к декартовому представлению вектора
При задании вектора U в декартовых координатах в виде тройки {u x , u y , u z }, как следует из Рис. 5.2‑3, имеет место:
![]()
j = arc cos (u z ./ r );

В выражении (5.1-11) в качестве сомножителей выступают матрицы разных размерностей (3*3 и 4*4). Для того, чтобы найти их произведение, необходимо привести матрицы к одной размерности, т.е. матрицы размерности 3*3 необходимо расширить до размерности 4*4. Однако с расширением размерности не надо спешить. Пользуясь свойством ассоциативности произведения матриц, умножение матриц следует выполнять в последовательности, определенной скобками в ниже приведенной версии выражения (5.1-11):
(5.1-12)
Обозначение матрицы знаком «*» означает использование расширенной матрицы.
Такой прием позволяет уменьшить затраты времени на выполнение умножений матриц.
В выражении (5.1-11) произведение первых трех матриц обеспечивает переход от исходной системы координат к системе координат, «удобной» для заданного преобразования. Что касается произведения последних трех матриц, то они обеспечивают переход от «удобной» системы координат к исходной. По этому, используя свойство ассоциативности, выражение (5.1-11) можно представить как:
(5.1-13)
R 1 – матрица перехода от исходной к «удобной» системе координат;
R 1 -1 –матрица, обратная матрице R 1.
В некоторых случаях, с точки зрения затрат времени, реализация выражения (5.1-12), может быть предпочтительнее, чем реализация выражения (5.1-11). В свою очередь, может оказаться удобнее формировать матрицу R 1 -1 не через произведение трех матриц (см. выражение(5.1-13), а получить ее, рассчитав ее элементы как элементы матрицы, обратной матрице R 1.
Матрица, обратная заданной, может быть найдена следующим образом.
Из определения обратной матрицы следует, что матрица В является обратной по отношению к заданной матрице А, если имеет место равенства:
А*B =E ,
где Е – единичная матрица, имеющая вид:

Отсюда элементы обратной матрицы могут быть найдены из системы уравнений.
Часть 8 - интегрирование угловых скоростей, матрицы поворота
Часть 11 - интегрирование угловых скоростей, методы высших порядков (в разработке)
Интегрирование угловых скоростей с помощью матриц поворота
Продолжаем нашу предвыборную гонку - какой интегратор угловых скоростей займёт своё законное место у руля (в буквальном смысле) нашего изделия?
Мы уже накопали компромата на углы Эйлера-Крылова - это конечно уважаемые и достойные фамилии, но очень уж старенькие - задрать голову в зенит не могут, сразу начинает голова кружиться, да и подвешенные вниз головой резко теряют работоспособность. Да и вообще, уголовники (системы, основанные на углах) нам не нужны!
Сегодня мы рассмотрим матрицы поворота - 9 направляющих косинусов не могут ошибаться, не правда ли?
Кинематическое уравнение для связанных осей (когда угловая скорость проецируется на оси изделия) принимает вид:
Здесь A – матрица ориентации.
Для шага Δt мы можем записать приближенный метод интегрирования:
Этот метод – сугубо линейный, в нём применяются только сложения и умножения, особые точки отсутствуют как класс.
Один недостаток, который мы можем заметить «сходу» - это громоздкость: мы используем 9 чисел для представления матриц, а каждый шаг интегрирования по простейшему методу («первого порядка») требует 18 умножений и 18 сложений (без специализированного метода, «знающего» о единицах по главной диагонали – и вовсе 27 умножений). Если выписать по компонентам, мы получим (с верхним индексом 1 – новые значения, с верхним индексом 0 – старые):

Матричная запись позволяет скрыть эту внутреннюю сложность за красивыми выкладками, поэтому полезно иногда выписать вычисления «в лоб», чтобы помнить, с чем мы имеем дело.
Тем не менее, даже у самых старых бортовых вычислителей не возникло бы проблем, связанных с недостаточной производительностью – ну что такое 36 операций для компьютера!?
Нет, настоящая ахиллесова пята матриц поворота состоит в том, что по прошествии времени они перестают быть матрицами поворота, а вернуть их на путь истинный не так-то просто…
Пусть начальная матрица ориентации – единичная, то есть оси инерциальной и связанной систем координат совпадают:


После 72 шагов придём к матрице ориентации, равной:
тогда как должны были прийти к единичной матрице (поворот на 360 градусов!).
Можем записать эту матрицу, как произведение двух:
Вторая из них – матрица поворота по оси Z на угол 0,9° - такова накопленная ошибка интегрирования, вызванная слишком крупным шагом. В относительном выражении ошибка не так велика: 0,9/360 = 0,25%, что не так уж плохо, учитывая, сколь крупный шаг мы взяли.
А вот первая матрица – масштабирование по осям X, Y. Вектор с нулевой компонентой Z просто увеличит свою длину – зачастую это не так уж страшно – по крайней мере, это не изменит направление вектора. Точно так же, вектор (0;0;1) T останется без изменений – всё верно.
Самое интересное будет происходить с промежуточными векторами.
К примеру, вектор![]()
превратится в
он не только увеличивается в размерах, но и меняет направление из-за масштабирования! Раньше он «смотрел» под углом 45° к плоскости X-Y, а теперь – под углом 37° - ошибка составляет уже не 0,9°, а целых 8°!
В данном конкретном случае мы легко смогли факторизовать матрицу, вычленив из неё отдельно поворот и отдельно масштабирование. Когда мы можем это сделать – понятно, как исправить ситуацию – нужно оставить только матрицу поворота, а масштабирование убрать!
Но представим теперь, что после поворотов вокруг оси Z, мы осуществили ещё и поворот вокруг приборной оси X на 30 градусов:

Как из этого нагромождения чисел наиболее оптимально вычленить отдельно повороты, избавившись от других преобразований пространства – вопрос по-прежнему открытый…
Напомним, что столбцы матрицы ориентации – это координаты базисных векторов в инерциальной системе отсчета. Эти векторы должны иметь единичную длину и быть взаимно-перпендикулярными, то есть мы можем записать следующие «уравнения связи» (в данном случае двойка наверху – это возведение в степень):

Действительно: при 9 коэффициентах матрицы, мы должны иметь ровно 3 степени свободы, поэтому нам и нужны дополнительные 6 уравнений. Проверим, что происходит у нас:
Длина 1-го базисного вектора: 1,314
Длина 2-го базисного вектора: 1,243
Длина 3-го базисного вектора: 1,087
Угол между 1 и 2: 90°
Угол между 2 и 3: 103,47°
Угол между 1 и 3: 90°
Ортонормированный базис перестал быть таковым! Мы понимаем это, но как именно скорректировать 9 значений, чтобы он снова стал ортонормированным?
Можно применить старый добрый метод построения ортонормированного базиса. Исходные базисные векторы обозначим e 1 , e 2 , e 3 :
![]()
Преобразованный базис назовём n 1
, n 2
, n 3
.
Первый вектор мы нормируем:
![]()
Из второго вектора мы вычитаем его проекцию на первый, после чего тоже нормируем:
Наконец, из третьего вектора вычитаем его проекцию на первый и второй, после чего нормируем:

В этих формулах есть определённое лукавство: кажется, что мы задействовали все 9 исходных коэффициентов, чтобы получить новые 9, теперь уже ортонормированные. На самом деле, от e 3 вообще ничего не зависит! Сначала мы вычитаем из него всё лишнее, так, чтобы он шел по прямой, взаимно перпендикулярной n 1 , n 2 , а затем нормируем его длину – да от этого вектора живого места не остаётся! Мы с тем же успехом можем записать:
![]()
и получить абсолютно тот же самый результат! То есть, в действительности данный метод берёт первые 6 коэффициентов и напрочь выкидывает последние 3. Да и первые 6 оказываются неравнозначны: если первому столбцу мы доверяем «безоговорочно», то второму – только до тех пор, пока он не противоречит первому.
Попробуем процедуру нормировки на нашей матрице B:
При этом, как и следовало ожидать, n 3 получился одинаковым до последнего представимого знака после запятой, независимо от способа вычисления – через e 3 или через векторное произведение.
Сейчас нам повезло – мы идеально отнормировали матрицу, так что она выражает ровно то, что и должна – поворот на 0,9° вокруг оси Z и поворот на 30° вокруг оси X.
Но попробуем теперь зайти с обратной стороны – не e 1
, e 2
, e 3
, а e 3
, e 2
, e 1
. Получится вот что:

Вместо поворота на 30° по оси X, мы в этот раз получили поворот на 37°, реализовав фактически наихудший случай!
Правильным подходом было бы решение оптимизационной задачи: каждый коэффициент матрицы является суммой полезного сигнала и шума. Найти новые коэффициенты, выраженные через старые, таким образом, чтобы среднеквадратичная ошибка стремилась к минимуму. Но даже тогда мы не гарантируем наилучшей работы – кто сказал, что, используя приближенные матрицы конечного поворота, мы вносим именно случайную ошибку!?
Уточним, в чём наша проблема. Нам не хотелось выписывать точную матрицу конечного поворота, поскольку она выглядит примерно так:
(меняя порядок поворотов, будем получать разные матрицы W, но все они будут являться строго матрицами поворота)
Мы «из жадности» её упростили:

И обнаружили, что выкинутые нами слагаемые второго порядка малости приводят к изменению вида матрицы. В нашем примере поворота вокруг оси Z, получаем

Разложив в ряд Тейлора до 3-го порядка малости, имеем:

И снова мы наблюдаем похожий эффект: ошибка интегрирования на этот раз чрезвычайно мала, составляя менее угловой секунды, тогда как наиболее заметное искажение снова проявилось в масштабе. Кажется, что ошибка весьма мала – менее одной тысячной – но этого достаточно, чтобы вектор, направленный под углом 45° к плоскости XY, «прижался бы» к ней дополнительно на 1 угловую минуту.
Так что даже использование малого шага интегрирования и применение методов высокого порядка не решает проблему накопления «мусора» в матрице. И чем больше проходит времени, тем больше в матрице будет мусора, который мы сможем отбросить только вместе с полезными данными.
Всё сказанное не означает, что матрицы поворота абсолютно не годятся для интегрирования угловых скоростей. Их можно применить, если соблюдать определённую осторожность - обязательно предусмотреть процедуру "ортонормирования", но по возможности до неё не доводить - повсюду перейти на удвоенную или расширенную точность, уменьшить шаг интегрирования, использовать численные методы высокого порядка.
Но как мы узнаем в следующей главе, кватернионы свободны от большинства недостатков матриц поворота и выходят в этой битве победителями.
Продолжение следует...
Матрицей поворота
(или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что, в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в трёхмерном пространстве
Любое вращение в трехмерном пространстве может быть представлено как композиция поворотов вокруг трех ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трех матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x:
Вращение вокруг оси y:
Вращение вокруг оси z:
После преобразований мы получаем формулы:
По оси Х
x’=x;
y’:=y*cos(L)+z*sin(L) ;
z’:=-y*sin(L)+z*cos(L) ;

По оси Y
x’=x*cos(L)+z*sin(L);
y’=y;
z’=-x*sin(L)+z*cos(L);

По оси Z
x’=x*cos(L)-y*sin(L);
y’=x*sin(L)+y*cos(L);
z’=z;

Все три поворота делаются независимо друг от друга, т.е.
если надо повернуть вокруг осей Ox и Oy, вначале делается поворот вокруг оси Ox, потом применительно к полученной точки делается поворот вокруг оси Oy.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Геометрические преобразования в трёхмерном пространстве
Переход из одной прямолинейной координатной системы в трёхмерном пространстве к другой описывается в общем случае следующим образом:

или в матричном виде:

Рассмотрим матрицы, соответствующие следующим базовым геометрическим преобразованиям:
1. Повороты 



2. Растяжение (сжатие):

3. Отражение (зеркалирование)
- относительно плоскости XOY

- относительно плоскости YOZ

- относительно плоскости ZOX

4. Перенос (сдвиг, перемещение) на вектор 
Важно: преобразование точки (с сохранением расположения исходной системы координат) соответствует выполнению обратной операции по отношению к преобразованию системы координат. Например, поворот точки на некоторый угол по часовой стрелке вокруг оси X соответствует повороту системы координат против часовой стрелки на тот же угол.
Все остальные преобразования, кроме вышеперечисленных, относятся к сложным преобразованиям. Матрицы сложных преобразований получаются при помощи нахождения произведения матриц, соответствующих базовым геометрическим преобразованиям, которые необходимо осуществить для получения искомого сложного преобразования (*-умножение производится строго в том порядке, в котором эти базовые преобразования производятся, т.к. преобразования некоммутативны).
В качестве примера рассмотрим сложное преобразование, заключающееся во вращении на угол вокруг прямой, проходящей через точку T(X, Y, Z) и имеющую направляющий вектор V(l, m, n) , причемl 2 +m 2 +n 2 =1 , т.е. вектор V является единичным.
Необходимо разложить преобразование на ряд элементарных шагов (базовых преобразований).
Цель: развернем систему координат так, чтобы ось Z совпала с V , после чего поворот на угол будет возможно произвести путем осуществления базового преобразования — поворота на этот угол вокруг оси Z .
Для достижения этой цели выполним следующую последовательность базовых преобразований:

Перспективное изображение возникает при центральном проецировании, т.е. когда центр проецирования (глаз наблюдателя) находится на конечном расстоянии от экрана.
Матрица перспективного преобразования с проецированием на плоскость XOY :
 ,
,
где С(0, 0, c) — точка расположения наблюдателя (центр проецирования). Плоскость проецирования, т.е. экран, совпадает с координатной плоскостью XOY
.
3.2. Трехмерные преобразования и проекции
Рассмотрим трехмерную декартовую систему координат, являющуюся правосторонней .
Матрица вращения
Примем соглашение, в соответствии с которым будем считать положительными такие повороты, при которых (если смотреть с конца полуоси в направлении начала координат) поворот на 90° против часовой стрелки будет переводить одну полуось в другую. На основе этого соглашения строится следующая таблица, которую можно использовать как для правых, так и для левых систем координат:

Рис. 3.6. Трехмерная система координат
Аналогично тому, как точка на плоскости описывается вектором (x,y ), точка в трехмерном пространстве описывается вектором (x,y,z ).
Как и в двухмерном случае, для возможности реализаций трехмерных преобразований с помощью матриц перейдем к однородным координатам:
[x,y,x ,1] или [X,Y,Z,H ]
[x*,y*,z* 1] = , где Н ¹1, Н ¹0.
Обобщенная матрица преобразования 4´4 для трехмерных однородных координат имеет вид
е. [x,y,z, 1]*T(Dx,Dy,Dz)= [x+Dx,y+Dy,z+Dz, 1].
2. Трехмерное изменение масштаба.
Рассмотрим частичное изменение масштаба. Оно реализуется следующим образом:
Такой же результат можно получить при равных коэффициентах частичных изменений масштабов. В этом случае матрица преобразования такова:
4. Трехмерное вращение
Двухмерный поворот, рассмотренный ранее, является в то же время трехмерным поворотом вокруг оси Z . В трехмерном пространстве поворот вокруг оси Z описывается матрицей
| R z ()= |
Матрица поворота вокруг оси X имеет вид
Подматрицу 3´3 называют ортогональной, так как ее столбцы являются взаимно ортогональными единичными векторами.
Матрицы поворота сохраняют длину и углы, а матрицы масштабирования и сдвига нет.
скачать
Реферат на тему:
Матрица поворота
План:
- Введение
- 1Матрица поворота в двумерном пространстве
- 2Матрица поворота в трёхмерном пространстве
- 3Свойства матрицы поворота
Литература
Введение
Матрицей поворота (или матрицей направляющих косинусов ) называется матрица, умножение любого вектора на которую не меняет его длины.
1.
Матрица вращения
Матрица поворота в двумерном пространстве
В двумерном пространстве поворот можно описать одним углом θ со следующей матрицей линейного преобразования в декартовой системе координат:

Положительным углам при этом соответствует вращение против часовой стрелки в обычной, правосторонней системе координат, и по часовой в левосторонней системе координат.
Сам поворот происходит путём умножения матрицы поворота на вектор, описывающий вращаемую точку:
.
2. Матрица поворота в трёхмерном пространстве
Матрицами вращения вокруг оси декартовой правой системы координат на угол α
в трёхмерном пространстве являются:
 ,
,
 ,
,
 ,
,
В трёхмерном пространстве для описания поворота можно использовать

Матрицы поворота вектора в декартовой системе координат, соответствующие первым двум способам задания поворота:
Однако, поскольку умножение матриц не коммутативно, то есть: , следовательно, положение системы координат после поворота вокруг трех осей будет зависеть от последовательности поворотов, то существует 6 различных видов матрицы поворота:
- 1) Поворот около осей: X -> Y -> Z
- 2) Соответственно: X -> Z -> Y
- 3) Y -> X -> Z
- 4) Y -> Z -> X
- 5) Z -> X -> Y
- 6) Z -> Y -> X
Получить же нужную матрицу можно путем последовательного перемножения матриц поворота около одной оси (приведенных выше) в соответствии с желаемым порядком.
3. Свойства матрицы поворота
Если - матрица, задающая поворот вокруг оси на угол φ, то:
Литература
- Лурье А. И.
Аналитическая механика - М.:Физматлит - 1961 г. - 824 с.
8.1.1. Преобразование координат в трехмерном пространстве.
B основе программ аффинных преобразований пространственных объектов, а также их проецирования на картинную плоскость лежит аппарат однородных координат (см., например, СПИСОК ЛИТЕРАТУРЫ). При этом все необходимые для построения проекции и установления нужного ракурса преобразования координат описываются матрицами размером 4 ´ 4 и представляются в виде суперпозиции некоторых основных преобразований: переноса точки в пространстве на фиксированный вектор, поворота вокруг указанной оси на заданный угол, масштабирования вдоль какой-либо оси, сдвига, перспективы и проецирования на одну из главных координатных плоскостей.

Рис.8.1. Декартова система координат, проекция P’ точки P на плоскость XZ, сетка, на которой задана поверхность, и сечения, параллельные плоскостям XZ и YZ.
Основные преобразования координат. Pассмотрим некоторую декартову систему координат (рис.8.1). Любая точка пространства представляется в ней вектор-матрицей вида (х у z). Mы будем пользоваться однородными координатами точки в пространстве (х у z 1).
B качестве картинной плоскости выберем плоскость XZ, описываемую уравнением Y = 0. Проекция точки объекта на эту плоскость получается в результате умножения (х у z 1) ×A, где
задает преобразование проецирования на плоскость XZ.
Поворот вокруг заданной оси (X, Y и Z соответственно) на указанный угол a описываются следующими матрицами:
где а = sin a, b = соs a. Положительным считается поворот в направлении против часовой стрелки, если смотреть с конца оси, вокруг которой поворачивается объект.
Mатрицы преобразований переноса на фиксированный вектор и масштабирования имеют следующий вид:
Здесь (t x , t y , t z) – вектор переноса; s x , s y , s z — масштабные множители вдоль осей X, Y и Z соответственно, 1/s – множитель общего масштабирования.
Сдвиг заключается в том, что одна из координат точки (зависимая координата) изменяется на величину, пропорциональную одной из двух оставшихся координат (сдвигающей координате). Пусть зависимой координатой будет координата X, а сдвигающей – координата Y, тогда матрица сдвига будет иметь вид:
где F – коэффициент сдвига. Проекцию точек объекта на плоскость XZ из центра проекции C можно получить с помощью преобразования центрального проецирования. Eго матрица:
Здесь центр проекции лежит на оси Y и имеет Y-координату, равную (-H), где H > 0 (см. рис.8.1).
C помощью основных преобразований координат можно получить практически произвольные плоские геометрические проекции.
Pассмотрим сначала случай параллельного проецирования. В зависимости от того, какой угол образует направление проецирования с картинной плоскостью, параллельные проекции делятся на прямоугольные (например, аксонометрические проекции) и косоугольные. B случае прямоугольных проекций направление проецирования перпендикулярно картинной плоскости. В случае косоугольных проекций направление проецирования образует с картинной плоскостью угол, отличный от прямого. Более подробные сведения об этих типах проекций можно найти, например, в СПИСОК ЛИТЕРАТУРЫ.
Более общие аксонометрические проекции можно получить с помощью двух последовательных поворотов объекта (сначала вокруг оси Z на некоторый угол Az, а потом вокруг оси X на угол Aх) и затем ортогонального проецирования на плоскость XZ. Для двух наиболее распространенных типов аксонометрических проекций — изометрии и диметрии — углы поворота имеют следующие значения: Az = -45 ° , Aх = 35 ° и Az = -20 ° , Aх = 20 ° .
Hа рис.8.2 приведены примеры изометрической и диметрической проекций одной и той же поверхности, показано также как при этом проецируются на картинную плоскость оси декартовой системы координат.
Для построения косоугольных проекций удобно воспользоваться преобразованием сдвига. Одну из косоугольных проекций, например, можно построить следующей последовательностью преобразований:
1. сдвиг, в котором зависимой осью является ось X, сдвигающей осью — ось Y; коэффициент сдвига F = 1 в случае, если задана «положительная» проекция (рис.8.3, б), и F = -1, если требуется «отрицательная» проекция (рис.8.3, а);
2. сдвиг, в котором зависимой является ось Z, сдвигающей — ось Y и коэффициент сдвига F = 1;
3. проецирование на плоскость XZ.
B случае если ни одна из упомянутых стандартных параллельных проекций (изометрия, диметрия и косоугольная проекция) по каким-либо причинам не устраивает, можно построить требуемую проекцию с помощью переноса, поворота, масштабирования и сдвига.
Используя эти преобразования, можно также расположить нужным образом изображаемый объект в пространстве и затем построить какую-либо стандартную проекцию.

Рис.8.2. Диметрическая и изометрическая проекции поверхности, а также осей декартовой системы координат.
C помощью основных преобразований координат легко также формируется преобразование, которое позволит получать центральную проекцию объекта из произвольного центра проекции на плоскость, проходящую через начало координат перпендикулярно лучу зрения. Параллельная проекция тоже может быть задана по-другому — вектором направления проецирования, начало которого лежит в точке (0,0,0), а конец определяется программистом.
Tаким образом, для построения произвольной проекции графического объекта достаточно сформировать матрицу преобразования, являющегося суперпозицией перечисленных выше основных преобразований координат. Умножая матрицу координат произвольной точки справа на матрицу результирующего преобразования, получим координаты проекции этой точки на картинную плоскость в соответствии с выбранным способом проецирования.

Рис.8.3. «Отрицательная» (а) и «положительная» (б) косоугольные проекции поверхности, а также осей осей декартовой системы координат.
Далее описаны программы, реализующие основные преобразования координат, некоторые стандартные типы проекций, а также другие средства, необходимые для построения произвольных плоских геометрических проекций объектов.
Программы преобразований. Чтобы построить желаемую проекцию трехмерного объекта, нужно задать соответствующее преобразование.
Программы, определяющие преобразования, являются по сути установочными. Последовательность обращений к ним задает результирующее преобразование, соответствующее некоторому способу проецирования. Программы рисования будут использовать подготовленную матрицу преобразования для изображения объектов в выбранной проекции.
Kаждая из программ, устанавливающих свое преобразование, формирует матрицу размером 4 ´ 4 и умножает ее слева на матрицу текущего преобразования. B результате преобразования будут выполняться в том порядке, в котором они задавались. Hачальные установки выполняет программа INIT, которая формирует единичную матрицу. Обращение к ней отменяет уже накопленное преобразование. Очевидно, когда требуется получить новое результирующее преобразование, необходимо начинать с обращения к этой программе.
Получать некоторые стандартные проекции графических объектов позволяют программы ISOMET, DIMET, CABIN, VIEW, AXONOM. Однако иногда необходимо предварительно преобразовать объект (расположить некоторым образом в пространстве). Для этой цели можно воспользоваться программами, задающими поворот, растяжение, перенос, сдвиг. Это программы: TDROT, TDSCAL, TDTRAN, SHEAR.
Любое текущее преобразование можно сохранить (программа SAVETR) и при желании восстановить (программа SETTR). Bообще с помощью программы SETTR можно установить в качестве текущего преобразования произвольное преобразование, расширив тем самым круг основных преобразований координат.
Программа INIT производит инициализацию результирующего преобразования. Программа без параметров.
Программа TDTRAN(DX, DY, DZ) задает перенос объекта в пространстве относительно начала координат. Параметры программы DX,DY, DZ определяют вектор переноса.
Программа TDROT(NAXES,ALPHA) задает поворот системы координат относительно указанной оси на заданный угол. Eе параметры:
NAXES
номер оси, относительно которой выполняется поворот:
Кроме того, если NAXES < 0, угол поворота считается заданным в радианах,
NAXES > 0 — в градусах;
ALPHA
угол поворота:
ALPHA > 0 — поворот выполняется против часовой стрелки, относительно оси, вокруг которой выполняется поворот;
ALPHA < 0 — поворот выполняется по часовой стрелке.
Программа TDSCAL(NAXES,SCALE) позволяет выполнить растяжение (сжатие) вдоль указанной оси и, возможно, симметричное отражение объекта. Параметры программы следующие:
NAXES
номер оси, вдоль которой выполняется растяжение (сжатие):
SCALE
коэффициент растяжения (сжатия):
SCALE ³ 1 — растяжение в SCALE раз,
SCALE О (0,1) — сжатие в 1/SCALE раз,
SCALE < 0 симметричное отражение относительно соответствующей координатной плоскости или начала координат и растяжение в |SCALE| раз или сжатие в 1/|SCALE| раз.
Программа SHEAR(I,J,F) определяет сдвиг. Параметры программы:
I
номер сдвигающей координаты:
J
номер зависимой координаты;
F
коэффициент сдвига.
При I = J данное преобразование вырождается в преобразование масштабирования вдоль I-ой оси с коэффициентом растяжения равным (F+1).
Программа ISOMET формирует матрицу результирующего преобразования для получения изометрической проекции с учетом текущего преобразования.
6.Перенос и повороты в трехмерном пространстве.
Программа без параметров.
Программа DIMET позволяет сформировать матрицу результирующего преобразования для получения диметрической проекции с учетом текущего преобразования. Программа без параметров.
Программа CABIN(J) позволяет сформировать матрицу результирующего преобразования для получения косоугольной проекции с учетом текущего преобразования. Параметр программы J определяет вид косоугольной проекции. При J = 1 получается положительная проекция, а при J = -1 — отрицательная проекция.
Программа VIEW(X,Y,Z) позволяет сформировать матрицу центрального проецирования на плоскость, перпендикулярную лучу зрения. Параметры программы:
X,Y,Z
координаты центра проекции (точки зрения).
Изменяя координаты точки зрения можно получать различные проекции объекта. Для получения нужного ракурса иногда бывает удобнее перемещать в пространстве сам объект, оставляя центр проекции неподвижным. Этого можно достичь обращением к программам TDROT и TDTRAN (до вызова программы VIEW).
При обращении к программе VIEW надо следить, чтобы центр проекции не оказался внутри изображаемого объекта, иначе результаты работы программы рисования THREED будут непредсказуемы.
Программа AXONOM(X,Y,Z) формирует матрицу результирующего преобразования для получения аксонометрической проекции с учетом текущего преобразования. Hаправление проецирования определяется вектором, соединяющим точку (X,Y,Z) с началом координат.
A
одномерный массив длины 16.
Программа SETTR(A) позволяет занести в матрицу текущего преобразования содержимое заданного массива A. Предполагается, что в массиве A последовательно записаны столбцы матрицы размером 4 ´ 4.
Bспомогательные и служебные программы.
Программа HCUNIT(A) формирует единичную матрицу A размером 4 ´ 4.
Программа HCMULT(A,B) перемножает две квадратные матрицы четвертого порядка A ´B. Pезультат помещается на место матрицы A.
Программа HCPRSP(H) реализует преобразование центрального проецирования. Параметр H задает Y-координату центра проекции, расположенного на оси Y (H > 0).
Программа HCINV(X,Y,Z,XP,YP,ZP) вычисляет координаты (XP,YP,ZP) центра проекции с учетом обратного преобразования координат. Предварительно вычисляется матрица обратного преобразования.
Программа HCROT1(X,Y,Z) позволяет найти результирующее преобразование, переводящее двумя последовательными поворотами точку A(X,Y,Z) в точку с координатами  .
.
Рис.8.1. Декартова система координат, проекция P’ точки P на плоскость XZ, сетка, на которой задана поверхность, и сечения, параллельные плоскостям XZ и YZ.

Рис.8.2. Диметрическая и изометрическая проекции поверхности, а также осей декартовой системы координат.

Рис.8.3. «Отрицательная» (а) и «положительная» (б) косоугольные проекции поверхности, а также осей осей декартовой системы координат.
В двумерном пространстве поворот можно описать одним углом θ со следующей матрицей линейного преобразования в декартовой системе координат:
Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой в левосторонней системе координат.
Сам поворот происходит путём умножения матрицы поворота на вектор
Матрица поворота в трёхмерном пространстве
Матрицами вращения вокруг оси декартовой правой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x:
 ,
,
Вращение вокруг оси y:
 ,
,
Вращение вокруг оси z:
 ,
,
В трёхмерном пространстве для описания поворота можно использовать
Матрицы поворота вектора в декартовой системе координат, соответствующие первым двум способам задания поворота:
Однако, поскольку умножение матриц не коммутативно, то есть: , следовательно, положение системы координат после поворота вокруг трех осей будет зависеть от последовательности поворотов, то существует 6 различных видов матрицы поворота:
1) Поворот около осей: X -> Y -> Z
2) Соответственно: X -> Z -> Y
3) Y -> X -> Z
4) Y -> Z -> X
5) Z -> X -> Y
6) Z -> Y -> X
Получить же нужную матрицу можно путем последовательного перемножения матриц поворота около одной оси (приведенных выше) в соответствии с желаемым порядком.
Билет 33. Свойства обратной матрицы
33) Обра́тная ма́трица - такая матрица A −1 , при умножении на которую исходная матрица A даёт в результате единичную матрицу E :
1)![]() ,
где
обозначает
определитель.
,
где
обозначает
определитель.
2)для любых двух обратимых матриц A и B .
3)где * T обозначает транспонированную матрицу.
4)для любого коэффициента .
5)Если необходимо решить систему линейных уравнений Ax = b , (b - ненулевой вектор) где x - искомый вектор, и если A − 1 существует, то x = A − 1 b . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Матричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:
AX = B , где A - основная матрица системы, B и X - столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A − 1 - матрицу, обратную к матрице A :
Так как A − 1 A = E , получаем X = A − 1 B . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Билет 34. Теорема о связи решений однородной и неоднородной СЛАУ.
Неоднородная система: Ax=B, B≠0.
Однородная система: Ах=0.
Теорема: 1. Если вычесть два решения неоднородной системы, то получится решение однородной системы.
2. Если к решению неоднородной системы прибавить решение однородной системы, то получится решение неоднородной системы.
Доказательство:
1) с 1 ,с 2 – два решения неоднородной системы.
Ас 1 =В; Ас 2 =В. Из первой системы вычтем вторую систему: Ас 1 -Ас 2 =0; А(с 1 -с 2)=0; с 1 -с 2 – решение однородной системы.
2) Ас н =В – решение неоднородной системы.
Ас о =0 - решение однородной системы.
Ас н + Ас о =В. А(с н + с о)=В. с н + с о – решение неоднородной системы.
Билет 35. Несовместность СЛАУ. Метод Гауса.
Если система решений не имеет, то она называется несовместной.
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа:
1)На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
2)На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Уравнение y=kx+b называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой. k=tg(альфа).
Угол между двумя прямыми:
Первая прямая: L 1 , n 1 (p 1 ,q 1 ,r 1).
Вторая прямая: L 0 , n 0 (p,q,r).
L 1 // L 0 ; n 1 // n 0 ; p 1 /р=q 1 /q= r 1 /r – условие параллельности 2 прямых.
L 1 ﬩ L 0 ; n 1 ﬩n 0 ; (n 1 ,n)=0; pp 1 +qq 1 +rr 1 =0 – условие параллельности 2 прямых.
Cosφ=(n 1 ,n)/|n 1 |*|n 0 |
В плоскости Лобачевского две прямые могут либо пересекаться, либо могут быть параллельными в некотором направлении, либо расходящимися. Поэтому в плоскости Лобачевского существует три вида пучков прямых:
1) пучок прямых, пересекающихся в одной точке, называемой центром пучка; такой пучок называется центральным или эллиптическим;
2) пучок прямых, параллельных в заданном направлении некоторой прямой, называемой осью пучка; такой пучок называется параболическим;
3) пучок расходящихся прямых, перпендикулярных к некоторой прямой, называемой базой пучка; такой пучок называется гиперболическим.
Взаимное расположение прямых на плоскости.
Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.
1. Параллельные прямые линии.
Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.
Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если AB//CD то A 1 B 1 //C 1 D 1 ; A 2 B 2 //C 2 D 2 ; A 3 B 3 //C 3 D 3 (рис.33). В общем случае справедливо и обратное утверждение.
В двумерном пространстве поворот можно описать одним углом со следующей матрицей линейного преобразования в декартовой системе координат:
![]()
Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:
![]() .
.
Координаты (x",y") в результате поворота точки (x,y) имеют вид:
Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой стрелке в левосторонней системе координат.
[править] Матрица поворота в трёхмерном пространстве
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
· Вращение вокруг оси x:
 ,
,
· Вращение вокруг оси y:
 ,
,
· Вращение вокруг оси z:
 .
.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть на плоскость вращении со стороны полупространства, где значения координат оси, вокруг которой осуществляется поворот, положительные. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Свойства матрицы поворота.
Свойства матрицы поворота
Если - матрица, задающая поворот вокруг оси на угол ϕ, то:
· (след матрицы вращения)
· (матрица имеет единичный определитель).
· если строки (или столбцы матрицы) рассматривать как координаты векторов , то верны следующие соотношения):
o ![]()
· Матрица обратного поворота получается обычным транспонированием матрицы прямого поворота, т. о. .
24. Алгоритм Брезенхема для растеризации отрезка.
Алгоритм Брезенхе́ма (англ. Bresenham"s line algorithm ) - это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике - он был разработан Джеком Е. Брезенхэмом (Jack E. Bresenham) в компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера. Существует обобщение алгоритма Брезенхэма для построения кривых 2-го порядка.
Алгоритм
Отрезок проводится между двумя точками - (x 0 ,y 0) и (x 1 ,y 1), где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x 1 − x 0 превосходит вертикальное y 1 − y 0 , т.е. наклон линии от горизонтали - менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x 0 и x 1 , определить, какая строка y ближе всего к линии, и нарисовать точку (x ,y ).
Общая формула линии между двумя точками:
![]()
Поскольку мы знаем колонку x , то строка y получается округлением к целому следующего значения:
![]()
Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y 0 и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона
![]()
которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y , либо увеличиваем его на 1.
Что из этих двух выбрать - можно решить, отслеживая значение ошибки , которое означает - вертикальное расстояние между текущим значением y и точным значением y для текущего x . Всякий раз, когда мы увеличиваем x , мы увеличиваем значение ошибки на величину наклона s , приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y , поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot(x,y) рисует точку, а abs возвращает абсолютную величину числа:
function line(x0, x1, y0, y1) int deltax:= abs(x1 - x0) int deltay:= abs(y1 - y0) real error:= 0 real deltaerr:= deltay / deltax int y:= y0 for x from x0 to if error >= 0.5 y:= y + 1 error:= error - 1.0Проблема такого подхода - в том, что с вещественными величинами, такими как error и deltaerr, компьютеры работают относительно медленно. Кроме того, при вычислениях с плавающей точкой может накапливаться ошибка. По этим причинам, лучше работать только с целыми числами. Это можно сделать, если умножить все используемые вещественные величины на deltax. Единственная проблема - с константой 0.5 - но в данном случае достаточно умножить обе части неравенства на 2. Получаем следующий код:
function line(x0, x1, y0, y1) int deltax:= abs(x1 - x0) int deltay:= abs(y1 - y0) int error:= 0 int deltaerr:= deltay int y:= y0 for x from x0 to x1 plot(x,y) error:= error + deltaerr if 2 * error >= deltax y:= y + 1 error:= error - deltaxУмножение на 2 для целых чисел реализуется битовым сдвигом влево.
Теперь мы можем быстро рисовать линии, направленные вправо-вниз с величиной наклона меньше 1. Осталось распространить алгоритм на рисование во всех направлениях. Это достигается за счёт зеркальных отражений, т.е. заменой знака (шаг в 1 заменяется на -1), обменом переменных x и y , обменом координат начала отрезка с координатами конца.
[править] Рисование линий
Реализация на C++:
Void drawLine(int x1, int y1, int x2, int y2){ int deltaX = abs(x2 - x1); int deltaY = abs(y2 - y1); int signX = x1 < x2 ? 1: -1; int signY = y1 < y2 ? 1: -1; int error = deltaX - deltaY; for (;;) { setPixel(x1, y1); if(x1 == x2 && y1 == y2) break; int error2 = error * 2; if(error2 > -deltaY) { error -= deltaY; x1 += signX; } if(error2 < deltaX) { error += deltaX; y1 += signY; } }}
25. Алгоритм Брезенхема для растеризации окружности.
Рисование окружностей
Также существует алгоритм Брезенхэма для рисования окружностей. По методу построения он похож на рисование линии. В этом алгоритме строится дуга окружности для первого квадранта, а координаты точек окружности для остальных квадрантов получаются симметрично. На каждом шаге алгоритма рассматриваются три пикселя, и из них выбирается наиболее подходящий путём сравнения расстояний от центра до выбранного пикселя с радиусом окружности.
// R - радиус, X1, Y1 - координаты центра int x:= 0 int y:= R int delta:= 2 - 2 * R int error:= 0 while (y >= 0) drawpixel(X1 + x, Y1 + y) drawpixel(X1 + x, Y1 - y) drawpixel(X1 - x, Y1 + y) drawpixel(X1 - x, Y1 - y) error = 2 * (delta + y) - 1 if ((delta < 0) && (error <= 0)) delta += 2 * ++x + 1 continue error = 2 * (delta - x) - 1 if ((delta > 0) && (error > 0)) delta += 1 - 2 * --y continue x++ delta += 2 * (x - y) y--
Void drawCircle(int x0, int y0, int radius) { int x = 0; int y = radius; int delta = 2 - 2 * radius; int error = 0; while(y >= 0) { setPixel(x0 + x, y0 + y); setPixel(x0 + x, y0 - y); setPixel(x0 - x, y0 + y); setPixel(x0 - x, y0 - y); error = 2 * (delta + y) - 1; if(delta < 0 && error <= 0) { ++x; delta += 2 * x + 1; continue; } error = 2 * (delta - x) - 1; if(delta > 0 && error > 0) { --y; delta += 1 - 2 * y; continue; } ++x; delta += 2 * (x - y); --y; }}
Алгоритм сглаживания Ву.
Алгоритм Ву - это алгоритм разложения отрезка в растр со сглаживанием. Был предложен У Сяолинем (Xiaolin Wu , отсюда устоявшееся в русском языке название алгоритма) в статье, опубликованной журналом Computer Graphics в июле 1991 года. Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхема без сглаживания.
Алгоритм
Горизонтальные и вертикальные линии не требуют никакого сглаживания, поэтому их рисование выполняется отдельно. Для остальных линий алгоритм Ву проходит их вдоль основной оси, подбирая координаты по неосновной оси аналогично алгоритму Брезенхема. Отличие состоит в том, что в алгоритме Ву на каждом шаге устанавливается не одна, а две точки. Например, если основной осью является Х , то рассматриваются точки с координатами (х, у) и (х, у+1) . В зависимости от величины ошибки, которая показывает как далеко ушли пиксели от идеальной линии по неосновной оси, распределяется интенсивность между этими двумя точками. Чем больше удалена точка от идеальной линии, тем меньше ее интенсивность. Значения интенсивности двух пикселей всегда дают в сумме единицу, то есть это интенсивность одного пикселя, в точности попавшего на идеальную линию. Такое распределение придаст линии одинаковую интенсивность на всем ее протяжении, создавая при этом иллюзию, что точки расположены вдоль линии не по две, а по одной.

Результат работы алгоритма
Реализация в псевдокоде (только для линии по x):
function plot(x, y, c) is // рисует точку с координатами (x, y) // и яркостью c (где 0 ≤ c ≤ 1) function ipart(x) is return целая часть от x function round(x) is return ipart(x + 0.5) // округление до ближайшего целого function fpart(x) is return дробная часть x function draw_line(x1,y1,x2,y2) is if x2 < x1 then swap (x1, x2) swap (y1, y2) end if dx:= x2 - x1 dy:= y2 - y1 gradient:= dy ÷ dx // обработать начальную точку xend:= round(x1) yend:= y1 + gradient × (xend - x1) xgap:= 1 - fpart(x1 + 0.5) xpxl1:= xend ypxl1:= ipart(yend) plot(xpxl1, ypxl1, 1 - fpart(yend) × xgap) plot(xpxl1, ypxl1 + 1, fpart(yend) × xgap) intery:= yend + gradient // первое y-пересечение для цикла // обработать конечную точку xend:= round(x2) yend:= y2 + gradient × (xend - x2) xgap:= fpart(x2 + 0.5) xpxl2:= xend // будет использоваться в основном цикле ypxl2:= ipart(yend) plot(xpxl2, ypxl2, 1 - fpart(yend) × xgap) plot(xpxl2, ypxl2 + 1, fpart(yend) × xgap) // основной цикл for x from xpxl1 + 1 to xpxl2 - 1 do plot(x, ipart(intery), 1 - fpart(intery)) plot(x, ipart(intery) + 1, fpart(intery)) intery:= intery + gradient repeatend function26. Алгоритмы закрашивания.
Алгоритм закрашивания
Алгоритм закрашивания очень часто используется в компьютерной графике для закрашивания фигур имеющих границы. Так же этот алгоритм может иметь и другое применение например его можно использовать для нахождения центра масс тела по его изображению.
Алгоритмы двумерной растровой графики: закрашивание
Рассмотрим алгоритмы закрашивания произвольного контура, который уже нарисован в растре. Сначала находится пиксель внутри контура фигуры. Цвет этого пикселя изменяем на нужный цвет заполнения. Потом проводится анализ цвета всех соседних пикселей. Если цвет некоторого соседнего пикселя не равен цвету границы контура или цвету заполнения, то цвет этого пикселя изменяется на цвет заполнения.
Простое рекурсивное заполнение.
Procedure PixelFill (x, y, BColor, Color: Integer);
{x, y – координаты затравочной точки, BColor – цвет границы,
Color – цвет заполнения}
C:=GetPixel (x,y) {анализируем текущий цвет пикселя}
if (C<>BColor) and (C<>Color) then
PutPixel (x, y, Color);
PixelFill (x+1, y, BColor, Color);
PixelFill (x, y+1, BColor, Color);
PixelFill (x-1, y, BColor, Color);
PixelFill (x, y-1, BColor, Color);
Этот алгоритм не оптимизирован относительно использования стековой памяти и является одним из самых медленных алгоритмов закрашивания (в среднем только один из четырёх вызовов используется для закрашивания). Алгоритм не может заполнить области, ограниченные цветом заполнения. Можно построить подобный алгоритм и без рекурсии, если вместо стека использовать массивы.
Алгоритм закрашивания линиями.
1. Имеется затравочная точка с координатами (x st , y st) и начальное направление действия рекурсивных вызовов dir=1 . Параметры левой и правой границы вначале совпадают с координатой затравочной точки: x PL = x st , x PR = x st . Вызывается процедура LineFill , в которой:
2. Находятся x L и x R – левая и правая границы, между которыми проводится текущая горизонтальная линия.
3. Делается приращение у=у+dir и, между x L и x R , анализируется цвет пикселей над линией. Если он не совпадает с цветом заполнения, процедура LineFill вызывается рекурсивно с dir = 1 и x PL = x L , x LR = x R .
4. Делается приращение y=y–dir и, начиная от x L до предыдущего значения x PL анализируется цвет пикселей под линией. Если цвет пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и x PL = x L , x PR = x R .
5.
Продолжая по той же горизонтали от предыдущего x PR до x R анализируется цвет под
линией. Если цвет какого-либо пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1
и x PL = x L , x PR = x R .
Ниже приведен пример реализации этого алгоритма на языке С++:
void LineFill (int x, int y, int dir, int xPL, int xPR)
// в этой переменной будет храниться цвет пикселя
// УСТАНАВЛИВАЕМ ТЕКУЩИЕ ГРАНИЦЫ xL И xR
color = GetPixel (--xL,y);
// xL=xL-1 помещается в вызов функции
while (color != bcolor); // bcolor – цвет границы
color = GetPixel (++xR,y);
while (color !=bcolor);
Line (xL,y, xR,y, Mycolor);
//это может быть любая функция рисования линии
// АНАЛИЗИРУЕМ ПИКСЕЛИ НАД ЛИНИЕЙ
for (x=xL; x<=xR; x++) {
color = GetPixel (x, y+dir);
if (color !=bcolor)
x = LineFill (x, y+dir, dir, xL, xR);
// АНАЛИЗИРУЕМ ПИКСЕЛИ ПОД ЛИНИЕЙ СЛЕВА
for (x=xL; x<=xPL; x++) {
color = GetPixel (x, y-dir);
if (color !=bcolor)
// АНАЛИЗИРУЕМ ПИКСЕЛИ ПОД ЛИНИЕЙ СПРАВА
for (x=xPR; x<=xR; x++) {
color = GetPixel (x, y-dir);
if (color !=bcolor)
x = LineFill (x, y–dir, –dir, xL, xR);
В программах функция LineFill вызывается следующим образом:
LineFill (xst, yst, 1, xst, xst);
Совершенно очевидно, что существуют и другие эффективные алгоритмы заполнения. Например, алгоритмы заполнения, которые используют математическое описание контура, связаны с конкретной формой того полигона, который должен быть заполнен (например, прямоугольник или окружность). При этом контур может совсем не выводиться в растр. При этом в качестве заполнения легко использовать какую-либо текстуру.
27. Алгоритм отсечения отрезка Сазерленда-Коэна.
Алгоритм Коэна - Сазерленда (англ. Cohen-Sutherland ) - алгоритм отсечения отрезков, то есть алгоритм, позволяющий определить часть отрезка, которая пересекает прямоугольник. Был разработан Дэном Коэном и Айвеном Сазерлендом в Гарварде в 1966-1968 гг., и опубликован на конференции AFIPS в 1968.
Описание алгоритма

Алгоритм разделяет плоскость на 9 частей прямыми, которые образуют стороны прямоугольника. Каждой из 9 частей присваивается четырёхбитный код. Биты (от младшего до старшего) значат «левее», «правее», «ниже», «выше». Иными словами, у тех трёх частей плоскости, которые слева от прямоугольника, младший бит равен 1, и так далее.
Алгоритм определяет код конечных точек отрезка. Если оба кода равны нулю, то отрезок полностью находится в прямоугольнике. Если битовое И кодов не равно нулю, то отрезок не пересекает прямоугольник (т.к. это значит, что обе конечные точки отрезка находятся с одной стороны прямоугольника). В прочих случаях, алгоритм выбирает конечную точку, находящуюся вне прямоугольника, находит ближайшую к ней точку пересечения отрезка с одной из линий, образующей стороны прямоугольника, и использует эту точку пересечения как новую конечную точку отрезка. Укороченный отрезок снова пропускается через алгоритм.
Реализация алгоритма для трёхмерной модели идентична двумерной реализации, за исключением того, что вместо четырёхразрядного кода применяется шестиразрядный (дополнительные два бита глубины).
28. Алгоритм разбиения средней точкой.
